基本的な数式

基本的な数式表現の紹介。数式を書く人は最低限これらは覚えましょう。

基本的な数式表現

指数や分数などを含まない普通の文字式は、数式環境内にそのまま記述すると適切な書式になります。
ここでは、特殊な書き方をする表現を順番に紹介していきます。
EasyTeXの入力支援機能に含まれていないものもあります。簡単ですので覚えてしまいましょう。

指数（上付き文字）と下付き文字

指数（上付き文字）を書くには ^ を使います。指数部分は中括弧{ }で括って明確にします。
指数が一文字だけの場合は中括弧は省略できます。
また、下付き文字は _ を使って、同様に書くことができます。

e^{2x+1}, S_n=a_n-a_{n-1}

出力例
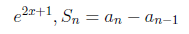
上付き・下付き文字の例

[小ワザ] 指数と下付き文字は同時に書くと、縦に揃って表示されます。
指数が下付き文字と揃って表示されるのを嫌う場合は、中括弧で括ると解決します。
下の例では、２つのパターンで別々に出力してみました（見やすいように画像にはスペースを入れてあります）

a_1^2+a_2^2+\cdots+a_n^2  {a_1}^2+{a_2}^2+\cdots+{a_n}^2

出力例
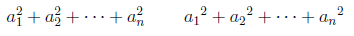
上付きと下付きをずらした例

基本的な数式

分数を表現するには2通りの表現方法があります。まず1つめは 1/2 という風にそのまま書いてしまう方法。これはそのまま 1/2 と出力されます。分数式が簡単な場合は案外たくさん使われます。
もう1つはコマンドを使ってしっかり分数を作る方法です。分数を作るコマンドの一般形は、\frac{分子}{分母} です。

\frac{1}{2}+\frac{1}{3}=\frac{5}{6}

出力例
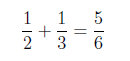
$fracコマンドの例$

一般的な関数

三角関数や対数関数などの各種関数は、イタリック表示を解除するためにそれ自体コマンドとして入力します。普通は関数の名前がそのままコマンドになっています。\関数の名前でいけます。
関数の変数部分は中括弧で括るか、半角スペースで区切ればうまく表示されます。
[注意] 関数と変数をつなげて書くとうまく認識されない場合があります。（たとえば"\cosx"と書くと"cosx"という存在しない関数として認識されてしまう）

\sin{x}+\tan x , \log_{10} x

出力例
一般的な関数の出力例

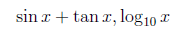
括弧

LaTeXには大きさが適切に変わる括弧があります。普通の括弧ももちろん入力できます。大きさを特に変えなくてもいい場合は、そのまま入力した方が格段に速いです。
さて、大きさが適切に変わる括弧のコマンドを普通の括弧( )で説明します。括弧開きが \left( になり、括弧閉じが \right) になります。
同様に大括弧は \left[ , \right] になります。中括弧を出力するときは注意が必要で、\left\{ , \right\} と中括弧の前に \ をはさんで書きます。大きさを変えないときの中括弧も \{ \} と書かないとコマンドの一部と見なされて出力されません。

\left( \frac{1}{2} \right) ^x

出力例
大きさの変わる括弧の出力例

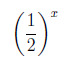
根号

ルート記号√は\sqrt{ }コマンドを使います。中括弧の中が根号の範囲で、ルートの上の棒がその分だけちゃんと伸びてきます。ちなみにsqrtというのはSquare rootの略です。また、一般のn乗根を書くときは中括弧{ }の前に[ ]をつけてその中に書きます。

\sqrt{x+2},\sqrt[3]{27}

出力例
根号の出力例

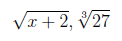
ギリシア文字

LaTeXではギリシア文字がコマンドで入力できます。「べーた」を変換してもβと書けますが、たくさん書くときには面倒になります。
EasyTeXではギリシア文字(G)にギリシア文字の一覧が用意されています。 LaTeXではepsilon(ε),theta(θ),pi(π),rho(ρ),sigma(σ),phi(φ)の小文字が２種類あって、微妙に形が異なります。コマンド名の頭にvarをつけて区別します。

特殊な文字修飾

文字にハット^ や、チルダ~ などをつけたいときもコマンドを使います。ただし、プライム（ダッシュ）だけは ' を普通に入力します。
TeX数式(M)＞上下につけるでコマンドの一覧があります。

a' , a'', \hat{a} , \check{a} , \tilde{a} , \dot{a}

出力例
特殊な文字修飾の出力例

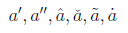
≪Prev ：数式の環境について | Next ：微分積分≫

(2007年10月21日)

▲このページのトップへ